#48/2023 - La scala logaritmica
Matematica
Parlando della scala Richter - quella che misura l’energia di un sisma - verrebbe da dire che tra un terremoto del 2° grado e uno del 4° grado, l’energia sprigionata sia raddoppiata.
Invece ci viene detto che l’energia sprigionata è molto maggiore, perché si tratta di una scala logaritmica.
Che cosa significa?
Oggi cercheremo di capirlo in modo semplice e con esempi, anche per chi ha poca familiarità con la matematica. Vedremo che la scala logaritmica ha diverse applicazioni, quindi vale la pena di familiarizzare con questo concetto per “afferrare” un po’ meglio le informazioni che ci arrivano dal mondo!
A cosa serve una scala logaritmica 📈
A volte le dimensioni di ciò che vogliamo misurare cambiano troppo rapidamente per essere visualizzate in un normale grafico. Le misurazioni possono cambiare molto poco all'inizio, ma poi aumentare rapidamente fino a valori estremi.
Prendiamo come esempio la crescita delle utenze di internet dal 1969. All’inizio erano pochissime e un grafico con la scala da 0 a 100 sarebbe stato sufficiente a rappresentarle per molti anni, fino al 1977. Dieci anni dopo sarebbe stato necessario aumentare la scala a 10.000.
Per l’anno 2012 avremmo dovuto aggiornare la scala fino al miliardo, e da qui in poi il numero di utenze si sarebbe stabilizzato intorno a questa cifra. La misurazione ha registrato una crescita di 9 ordini di grandezza…

Come funziona e come si legge una scala logaritmica 🤔
Immagina di essere in montagna, davanti a una salita che si fa sempre più ripida man mano che sali. Questo è ciò che accade a una quantità su una scala logaritmica: ogni passo che compi ti porta non a un incremento costante, ma a uno sempre più grande. Se su una scala lineare ogni tuo passo misura un metro, su una scala logaritmica il primo passo potrebbe misurare un metro, il secondo dieci, il terzo cento, e così via.
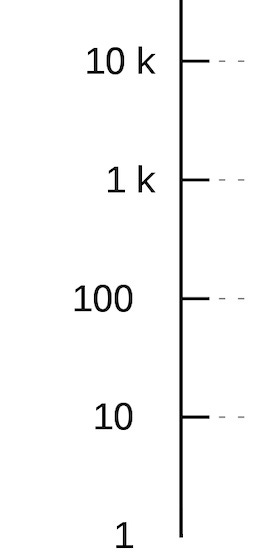
Rivediamo il grafico di prima, sulle utenze internet. Esso utilizza una scala lineare per gli anni, ma una scala logaritmica per il numero di utenze, sull'asse verticale. Qui ogni segmento è dieci volte maggiore del precedente.

In situazioni come questa, una scala lineare renderebbe difficile visualizzare i valori più piccoli, che verrebbero compressi vicino all'origine del grafico. La scala logaritmica invece comprime i valori più grandi e espande quelli più piccoli, così rende possibile visualizzare i pattern che altrimenti sarebbero difficili da rappresentare.
Se al posto della scala logaritmica avessimo utilizzato una scala lineare per rappresentare le utenze internet, ci sarebbe servito un grafico alto un miliardo di unità… e per un grafico così, o ti serve un foglio grande come un campo da calcio oppure dovendolo rappresentare in un foglio normale i dettagli iniziali sarebbero praticamente invisibili.
Con la scala logaritmica invece, manteniamo ben visibile il dettaglio di che cosa accade nella parte iniziale, quando la crescita si basa su numeri piccoli; allo stesso tempo riusciamo a vedere a quali valori arriva la crescita quando i numeri diventano enormi. Quindi siamo in grado di vedere l'intero intervallo di variazione in tutto il lasso di tempo.
Perché si chiama scala logaritmica? 📊
La scala logaritmica prende il nome dalla funzione matematica su cui si basa, il logaritmo. In termini semplici, il logaritmo è l'operazione inversa dell'elevamento a potenza.
Ad esempio:
se 101 = 10, allora il logaritmo in base 10 di 10 è 1
se 102 = 100, allora il logaritmo in base 10 di 100 è 2
se 103 = 1000, allora il logaritmo in base 10 di 1000 è 3
se 104 = 10000, allora il logaritmo in base 10 di 10000 è 4
e così via.
Ora immagina di avere un grafico in cui 1, 2, 3, 4 rappresentati sull’asse non sono i valori misurati ma sono i valori del logaritmo (quelli appena elencati sopra).
A questo punto avresti su quell’asse:
1 che rappresenta una quantità 10
2 che rappresenta una quantità 100
3 che rappresenta una quantità 1000
4 che rappresenta una quantità 10000.
Ed ecco che hai ottenuto una scala logaritmica.
In una scala logaritmica l’asse non aumenta linearmente ma secondo una base prefissata, di solito 10. Questo significa che anziché avere intervalli di uguale lunghezza che rappresentano un incremento di 1, ogni intervallo rappresenta un incremento che è una potenza della base. Nella scala logaritmica in base 10, un intervallo può rappresentare un aumento da 1 a 10, il successivo da 10 a 100, e così via.
Esempi di scale logaritmiche 💹
Ora che hai visto che la scala logaritmica consente di vedere l’andamento dei numeri più piccoli e più grandi contemporaneamente, è più facile capire perché alcuni dei più affascinanti fenomeni scientifici sono misurati con le scale logaritmiche. Ne cito qualcuno:
La potenza dei terremoti (misurata con la scala Richter: è una scala logaritmica)
La luminosità delle stelle (misurata con la Magnitudine: è una scala logaritmica)
L’intensità del suono (misurata in Decibel: è una scala logaritmica)
L’acidità di una soluzione (misurata con il pH: è una scala logaritmica)
Un’innumerevole quantità di dati statistici e indici, come la popolazione mondiale lungo la storia umana o le quotazioni del Bitcoin.

Relegare i logaritmi all’interno di un semplice concetto matematico, lasciandoli in pasto a matematici e ingegneri, è un peccato! Essi sono una chiave per leggere e decifrare la complessità della nostra realtà. La prossima volta che sentirai parlare di scale logaritmiche, ricorda che non sono solo per gli scienziati: sono dappertutto, e ora sai come leggerle e apprezzarle!

